\[mathjax\]
B-Spline曲線、Bazier曲線対照表
| B-Spline | Bazier | |
|---|---|---|
| 一般曲線表現(Bazier曲線を含む) | B-Splineの特殊系 | |
| 関数表現 | \[B(t) = \sum_{i=0}^{m-n-2} N_{i,n}(t) \cdot P_i \] | \[B(t) = \sum_{i=0}^{n} B_{i,n}(t) \cdot P_i \] |
| 基底関数 | B-Spline basis function de Boor Coxの漸化式 \[N_{j,0}(t) = \begin{cases} 1 & \text{if } t_j \leq t < t_{j+1} \cr 0 & \text{otherwise} \end{cases} \] \[N_{j,k}(t) = \frac{t – t_j}{t_{j+k} – t_j} N_{j,k-1}(t) + \frac{t_{j+k+1} – t}{t_{j+k+1} – t_{j+1}} N_{j+1,k-1}(t) \] | バーンスタイン基底関数 \[B_{i,n}(t) = C(n, i) \cdot (1-t)^{n-i} \cdot t^i \] |
| ノットベクトル | \[t_0 \leq t_1 \leq t_{m-1} \] 一様、あるいは、開一様である必要がある。 | なし。 |
| 制御点数・次数・ノットベクトル数の関係 | \[ n = m – N – 1 \] n:制御点数 m : ノットベクトル要素数 N:次数 | \[ n = N + 1 \] |
| 始点・終点通過性 | 開一様ノットベクトルに限り通過する。 | 常に通過する |
| 関係性 | \[ n = N + 1 \] を満たし、かつ、開一様ノットベクトルであれば、N次Bazier曲線に等しい | - |
| 局所性 | あり ある制御点数を移動させた場合の影響範囲は、前後N次数分のセグメントに限る | なし ( n = N + 1)であるため、一つの制御点の移動が曲線全体に影響する |
| 連続性 | 任意の制御点数を、任意の次数のB-Spline曲線で表現可能であり、定義式に従って長さ方向に2回微分可能なため、C2連続である。 | 任意の制御点数nを補間するためには、n-1の次数のベジェ曲線が必要である。この場合はC2連続である。一般的に計算量を鑑みて、3次ベジェ曲線でセグメントに区切って曲線表現することが一般的であるが、一般にC1連続である。C2連続であるためには制御点位置を調整する必要がある |
BSpline基底関数
B-Spline basis function
de Boor Coxの漸化式
\[N_{j,0}(t) = \begin{cases} 1 & \text{if } t_j \leq t < t_{j+1} \cr
0 & \text{otherwise} \end{cases} \]
\[N_{j,k}(t) = \frac{t – t_j}{t_{j+k} – t_j} N_{j,k-1}(t) + \frac{t_{j+k+1} – t}{t_{j+k+1} – t_{j+1}} N_{j+1,k-1}(t) \]
一般定義式は上記ですが、これに加えて分母がゼロになる場合の処理を追加する必要があります。
分母が0の場合には0となるようにハンドリングします。
fun basicFunc(t: Double, j:Int, k:Int, knot:D1Array<Double>):Double{
if (j < 0 || j > knot.size - k - 2){
throw IllegalArgumentException()
}
if (k == 0){
if ((knot[j] < t && t < knot[j+1]) || doubleEquals(knot[j], t)){
return 1.0
}else{
return 0.0
}
}else{
val left = if (doubleEquals(knot[j + k], knot[j])) 0.0 else ((t - knot[j]) / (knot[j+k] - knot[j]))
val right = if (doubleEquals(knot[j + k + 1], knot[j + 1])) 0.0 else ((knot[j+k+1] - t) / (knot[j+k+1]-knot[j+1]))
val ret = left * basicFunc(t, j, k - 1, knot) + right * basicFunc(t, j + 1, k - 1, knot)
if (ret.isNaN()){
println("t:$t, j:$j, k:$k")
println("${(t - knot[j])} * ${
basicFunc(
t,
j,
k - 1,
knot
)
} / ${(knot[j+k] - knot[j])} + ${(knot[j+k+1] - t)} * ${basicFunc(t, j + 1, k - 1, knot)} / ${(knot[j+k+1]-knot[j+1])}")
throw IllegalStateException("ret became Nan")
}
return ret
}
}
Kotlinで記載しているので適宜chatgptとかでconvertしてください
2次BSpline 基底関数 開一様ノットベクトル
制御点数6

3次BSpline 基底関数 開一様ノットベクトル
制御点数6
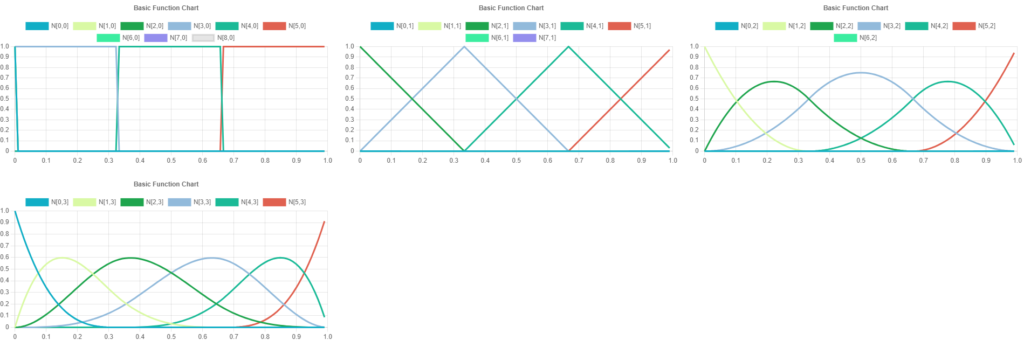
それぞれの基底関数が全体に対して0より大きい値を取らないため、局所性が存在することを表しています。
B-Spline, Bazier曲線
上がB-Spline曲線、曲率、曲率変化
下がBazier曲線、曲率、曲率変化
B-Spline曲線の方が急峻な曲率が表れやすく、一方でBazier曲線の方が全点を滑らかに接続する傾向にあることが分かります。
また、B-Spline曲線は一つの制御点の移動に対して局所性がありますが、Bazier曲線にそれはありません。また次数が増えるにつれてBazier曲線は一つの制御点に対する制御性が落ちており、任意の形状を作成することが困難です
NURBS
B-Splineをさらに一般化した曲線表示形式がNURBS (Non uniform rational basis spline)です。
\[ C(t) = \frac{\sum_{i=0}^{m-n-2} (N_{i,n}(t) \cdot w_i \cdot P_i)}{\sum_{i=0}^n (N_{i,n}(t) \cdot w_i)} \]
B-Spline対して、ノットベクトルが非一様でもよく、かつ、各制御点ごとに重みを設定可能です。結果として、 B-Splineよりも遥かに柔軟に様々な曲線をNURBSで表現することが可能です
重み
重みを調整することで制御点の曲線に対する影響度を調整することができます
ノットベクトル
ノットベクトルを非一様に持てるようになったことから、各制御点の影響を自由に定義できます。また、途中で多重度を持たせることで非曲率連続な形状を表現できます。
重み、ノットベクトルを調整することで概ね任意の曲線を表現できることからCAD等、多くのコンピュータグラフィックスにおける曲線表現の分野で採用されています。
B-Splineの次数は?
次数は一般的には3-5あたりの次数が選択されます。次数が増加するほど滑らかな曲線を表現できますが、次数の増加は一つの制御点数の影響度を低減させ、制御点の移動による曲線の変更というユーザビリティの低下につながります。また、次数の増加は内部的な計算量を増加させます。そのため、実用的に十分な3-5が現実的な落とし所として採用されることが多いようです。
Reference
コンピュータグラフィックス 基礎 第 6回 曲線・曲面の表現 「Bスプライン曲線」
https://mitani.cs.tsukuba.ac.jp/lecture/2020/cg\_basics/06/06\_slides.pdf
Tajima Robotics
Wikipedia BSpline
https://ja.wikipedia.org/wiki/B-%E3%82%B9%E3%83%97%E3%83%A9%E3%82%A4%E3%83%B3%E6%9B%B2%E7%B7%9A
自由曲線・曲面の滑らかさの理論および評価方法の考察と 3 次元 CAD への応用
https://www.graphicscience.jp/\_files/branch\_touhoku/2004-3a.pdf
Wikipedia NURBS
https://en.wikipedia.org/wiki/Non-uniform\_rational\_B-spline